INTRODUCCIÓN
El artículo 13 de la Norma para el Aseguramiento de la Calidad de la Información Estadística y Geográfica del Instituto Nacional de Estadística y Geografía (Norma) estipula que, para evaluar la calidad de la Información Estadística y Geográfica, las Unidades Administrativas, como mínimo, deberán calcular los indicadores de calidad y aplicar las metodologías de evaluación en los términos y periodicidad aprobados por el Comité. De acuerdo con el artículo 18 de la citada Norma, las Unidades Administrativas informarán al Comité los resultados de los indicadores y evaluaciones aplicados a los Procesos de Producción a su cargo, los cuales serán integrados en el Informe Anual de Resultados del Comité.
Considerando lo anterior y, para efectos de las atribuciones del Comité conforme al artículo 26 fracción IV de la Norma, se presenta la información del siguiente indicador de calidad.
1. MARCO DE REFERENCIA DEL INDICADOR
1.1 Nombre del indicador
Cota de Confianza de Precisión Posicional.
1.2 Acuerdos del CoAC mediante los cuales fue aprobado el indicador:
Acuerdo CAC- 005/03/2021 en la tercera sesión del 2021 del Comité de Aseguramiento de la Calidad.
1.3 Fecha de inicio para reportar el indicador:
Se calculará para los nuevos productos que se publiquen a partir del segundo trimestre de 2022.
Veracidad (precisión y confiabilidad)
1.5 Uso previsto del indicador:
El indicador "Cota de confianza de precisión posicional" es de uso combinado. Inicialmente será de uso interno y cuando así se juzgue, será también de uso externo (en la publicación de los resultados del Mapa Topográfico).
1.6 Fuentes de la metodología y/o estándares utilizados en el cálculo del indicador:
1.7 Persona(s) participante(s) en la integración de la ficha del indicador:
Unidad Administrativa o Grupo de trabajo.- Grupo de trabajo para la definición de indicadores de precisión para información geográfica.
Dr. Gerardo H. Terrazas González, Director de Análisis y Tratamiento Geoestadístico. Dirección General de Geografía y Medio Ambiente.
Ing. Ulises Pastrana Estrada, jefe del departamento de Mejora de la Gestión. Dirección General de Geografía y Medio Ambiente.
Dr. Enrique Muñoz Goncen, director general adjunto de Información Geográfica Básica. Dirección General de Geografía y Medio Ambiente.
Ing. Jazmin Karely Ahumada Ruiz, subdirectora de Especificaciones del Mapa Maestro México. Dirección General de Geografía y Medio Ambiente.
1.8 Medios de difusión:
Apartado de indicadores de calidad de la ficha de metadatos
1.9 Fecha de integración de la ficha:
04/06/2021. (Con base a la entrada en vigor de la NTPPIEG, se ajustaron algunos conceptos dentro de la ficha del indicador, los cuales no alteran en ningún sentido los aspectos técnicos del mismo; Dichos ajustes se aplicaron con fecha del 17/11/2021).
2. ESPECIFICACIONES TÉCNICAS DEL INDICADOR
2.1 Ámbito de aplicación:
Proceso de generación de información topográfica, levantamientos geodésicos, proceso de generación de información de recursos naturales y procesamiento de imágenes del territorio.
2.2 Objetivo del indicador:
Cota de Confianza de Precisión Posicional: Es el nivel superior de la precisión posicional estimada con un nivel de confianza del (1−α)% del RMSE estimado que ayuda a verificar si los insumos sirven para lograr una precisión deseada. A partir de estándares internacionales, específicamente ASPRS (American Society for Photogrammetry and Remote Sensing) que es el adoptado por la DGGMA, se usa como criterio de medición de calidad la Raíz del Error Cuadrado Medio (RMSE por sus siglas en inglés) entre los puntos de control, tanto en mediciones horizontales como verticales. La cota de Confianza de precisión posicional tiene como principales objetivos:
1. Determinar la precisión posicional del producto generado a partir de los insumos (por ejemplo, fotografías aéreas y/o imágenes satelitales).
2. Dado un requisito específico de RMSE horizontal a-priori por el usuario, apoyar en la toma de decisión para la colecta de los insumos.
2.3 Periodicidad:
Se calculará siempre que se presenten resultados del proceso de producción, ya sea parcial o en su totalidad.
2.4 Tiempo límite para el reporte del indicador:
Una vez entregados los resultados fotogramétricos y geodésicos, el cálculo del indicador deberá estar disponible en los metadatos en los 30 días naturales siguientes.
2.5 Periodo de referencia o ámbito de aplicación:
Se reportará el periodo de colecta de los insumos correspondientes. (inicio y fin).
2.6 Definiciones o conceptos relevantes:
La estimación de la cota usa como distribución base la normal que, a través del cálculo de las varianzas y desviaciones estándar, recae en una distribución Ji-Cuadrada. La base es conocer el proceso de inferencia para varianzas y desviaciones estándar de observaciones generadas por una distribución normal, principalmente a la estimación de intervalos de confianza.
2.7 Fórmula de cálculo:
Las variables de interés son las diferencias entre las mediciones en puntos seleccionados en las fotos (\( \hat{h}_{vi} \)) y una fuente de información de referencia (\( {h}_{vi} \)) donde se asume que los valores son verdaderos. El interés radica en la distribución de las diferencias entre las observaciones medidas y verdaderas de los puntos de control en
X, Y y Z; es decir, las diferencias son:
\( x_1, x_2, \dots, x_n \) en la dirección en el eje
X, donde \( x_i = (h_{xi} - \hat{h}_{xi} \)).
\( y_1, y_2, \dots, y_n \) en la dirección en el eje
Y, donde \( y_i = (h_{yi} - \hat{h}_{yi} \)).
\( z_1, z_2, \dots, z_n \) en la dirección en el eje
Z, donde \( z_i = (h_{zi} - \hat{h}_{zi} \)).
Se asume que las diferencias en todas las direcciones son resultados de variables aleatorias Normales;
X y Y \( \sim \mathcal{N}(0, \sigma^2)\); y \(Z \sim \mathcal{N}(0, \sigma_z^2) \).
El único parámetro a estimar es \( \sigma_v^2 \); y dado que se asume que la media es cero, el estimador de \( \sigma_v^2 \) está dado por \( \hat{\sigma}_v^2 = \frac{1}{n} \sum_{i=1}^{n} v_i^2 \), donde la
vi identifica las mediciones disponibles de cualquiera de las variables
xi, yi, zi. Para los fines a aplicación del estándar ASPRS es importante notar que la Raíz del Error Cuadrado Medio de la variable
v (RMSEv) está definido como \( RMSE_v = \sqrt{\sigma_v^2} \), por lo que el estimador es \( \widehat{RMSE}_v = \sqrt{\widehat{\sigma}_v^2} \) donde \( \hat{\sigma}_v^2 = \frac{1}{n} \sum_{i=1}^{n} v_i^2 \).
Es conocido que el estadístico \( gl \frac{\hat{\sigma}^2}{\sigma_v^2} = gl \frac{\widehat{RMSE^2}}{RMSE^2} \sim \chi^2_{gl} \) , donde:
gl=grados de libertad (en el presente proceso es igual al número de observaciones); \( \widehat{RMSE}^2 = \frac{1}{n} \sum_{i=1}^{n} v_i^2 \) de las mediciones disponibles - por ejemplo de proceso de Aerotriangulación - y \({RMSE^2} \) = Raíz del Error Cuadrado Medio al cuadrado que se asume en la distribución de los datos. Para el contexto de la cota de confianza, \( \sigma_v^2 = RMSE^2 \) se interpreta como en nivel de precisión que se desea verificar si las mediciones disponibles lo alcanzan (nivel de calidad).
Usando este resultado, la estimación de la cota (superior) al (1-α)% de confianza, es como sigue:
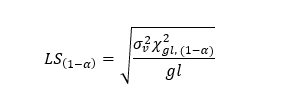
Si el \(\sqrt{\hat{\sigma}^2} = \widehat{RMSE} \leq LS_{(1 - \alpha)} \), se toma la decisión de que los insumos disponibles (mediciones) son suficientes para lograr el estándar de calidad dado por el RMSE "deseado".
2.8 Parámetro de interés
Índice
2.9 Fuentes de información del indicador
Para la cota de confianza de precisión posicional se requieren las diferencias entre las mediciones de puntos de control terrestre y los resultados de subprocesos derivados de las fuentes de información de los insumos, por ejemplo: fotografías aéreas e imágenes de satélite.
2.10 Nivel de agregación
El nivel de agregación es por polígono; sin embargo, se puede implementar a otros niveles de agregación de acuerdo a los objetivos de cada proceso de producción en donde la precisión posicional sea relevante.
2.11 Observaciones y/o especificaciones técnicas
La Cota de confianza es un valor estadístico que usa como principio la estimación de intervalos de confianza para medidas de dispersión en desviaciones estándar y varianzas. Es en efecto el límite superior de un intervalo de confianza de cola derecha al (1-α)%. La cola derecha da un valor límite (máximo) de calidad que se puede lograr en los productos generados a partir de los insumos (por ejemplo, fotografías aéreas y/o imágenes satelitales).
El proceso de cálculo asume que las diferencias observadas siguen una distribución normal con media cero, considerando igualdad de varianzas en las dimensiones X y Y. Para la dimensión Z (vertical) el proceso asume diferentes valores dependiendo la cobertura vegetal (áreas con vegetación y sin vegetación). Consultar (ASPRS 2014).
Con el cálculo del RMSE horizontal y vertical, y aplicando los resultados estadísticos correspondientes, se determinan las cotas de calidad en ambas dimensiones.
2.12 Valores de referencia o estándar de calidad utilizado
El estándar ASPRS presenta diferentes niveles de precisión de RMSE y asume valores aproximados en la fuente del insumo, como el tamaño de pixel en el terreno (GSD por sus siglas en inglés); sin embargo, no comenta sobre qué tan buena o mala es una estimación del indicador. Regularmente está a juicio de los expertos y los requerimientos para cada proceso de producción.
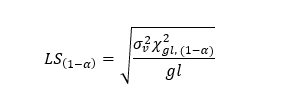 Si el \(\sqrt{\hat{\sigma}^2} = \widehat{RMSE} \leq LS_{(1 - \alpha)} \), se toma la decisión de que los insumos disponibles (mediciones) son suficientes para lograr el estándar de calidad dado por el RMSE "deseado".
Si el \(\sqrt{\hat{\sigma}^2} = \widehat{RMSE} \leq LS_{(1 - \alpha)} \), se toma la decisión de que los insumos disponibles (mediciones) son suficientes para lograr el estándar de calidad dado por el RMSE "deseado".